중앙값 이란?
중앙값이란 하나의 집단에서 작은 수부터 큰수를 순서대로 나열 하였을때 중앙에 위치되어 있는 수를 얘기한다.
집단 A : 1,2,3,4,5
집단 B : 3,4,5,6,7,8
이처럼 집단 A가 있고 집단 B가 있을때 A는 5개의 수가 있고 B에는 6개의 수가 있다.
A의 중앙값은 중앙에 위치한 3이 중앙값이고 B의 중앙값은 가운데 위치해 있는 5와 6의 평균인 5.5가 된다.
우리가 주로 하나의 집단에서 대표되는 값으로 특정 집단의 평균을 많이 사용하는데
평균은 모집단에서 가지고 있는 데이터의 수와 최대값과 최소값의 영향을 많이 받기 때문에 이때 평균을 대신 하여서 중앙값을 사용하는 경우가 있다.
EX) A 집단의 나이는 각각 25,30,35,40,70 일때 평균은 40세가 되는데 이는 70으로 인해 평균이 영향을 크게 받았다고 볼 수 있다 이때 우리는 이 집단의 대표를 중앙값이 35로 볼 수도 있다.
분위수 란?
분위수란 1사분위수, 2사분위수, 3사분위수가 있고 이들의 값은 하나의 집단에 작은 수부터 큰수 까지 나열 하였을때 1/4 위치에 있는 수, 2/4 위치에 있는 수, 3/4 위치에 있는 수를 각각 1사 분위수, 2사 분위수, 3사 분위수라고 표현 한다.
이때 1사 분위수 부터 3사 분위수 사이에 있는 범위차를 IQR 이라고 한다.
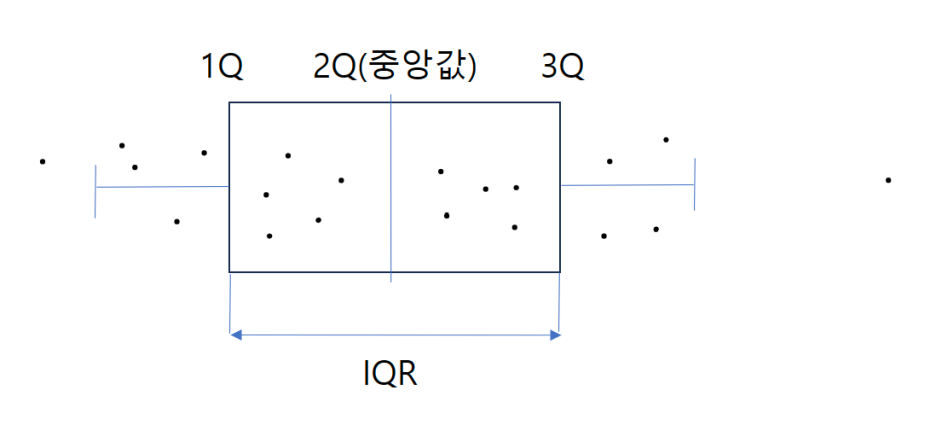
위에 총 20개의 점이 있고 짝수 이므로 위에서의 집단 B와 같이 점 사이에 있는 값이 2Q(중앙값)이 된다.
이때 1Q와 3Q 는 중앙값을 기준으로 집단을 반으로 나눈뒤 반으로 나누어진 집단에서(10개의 점)의 중앙값을 찾으면 동일하게 점 사이(5,6번째 점)의 값이 각각 1Q, 3Q가 된다.
3Q와 1Q의 차이를 IQR 이라고 하고 이는 3Q - 1Q로 표현 할 수 있다.
EX)1Q의 값이 10, 3Q의 값이 30 일때 IQR은 20이라는 값을 가진다.
이상치란 집단안에 분포해있는 값중에 값이 너무 작거나 너무 큰 점들을 이야기 하며 이러한 점들은 평균에 큰 영향을 미쳐 이상치 혹은 영향점 이라고 얘기를 한다.
1Q를 기준으로 IQR * 1.5 를 뺀 값보다 작을 경우
3Q를 기준으로 IQR * 1.5 를 더한 값보다 클 경유를 이상치라고 얘기 할 수 있고 이때 값 1.5는 바뀔수 있다.
수식으로 풀어보면 이상치 X의 값은
X < Q1 - (1.5 * IQR) - X는 1사 분위수 빼기 1.5 * IQR 보다 작은 값
X > Q3 + (1.5 * IQR) - X는 3사 분위수 더하기 1.5 * IQR 보다 큰 값
으로 풀이 할 수 있고, 이상치는 하나의 집단에 여러개가 분포해 있을 수 있고 없을 수도 있다.