R²(결정계수) 란?
우리가 만든 모델(선형 회귀 계수)이 얼마나 성능이 좋은가를 확인하기 위해서 사용되는 지표로써
우리의 모델이 종속변수를 얼마나 잘 설명 하는지를 얘기함
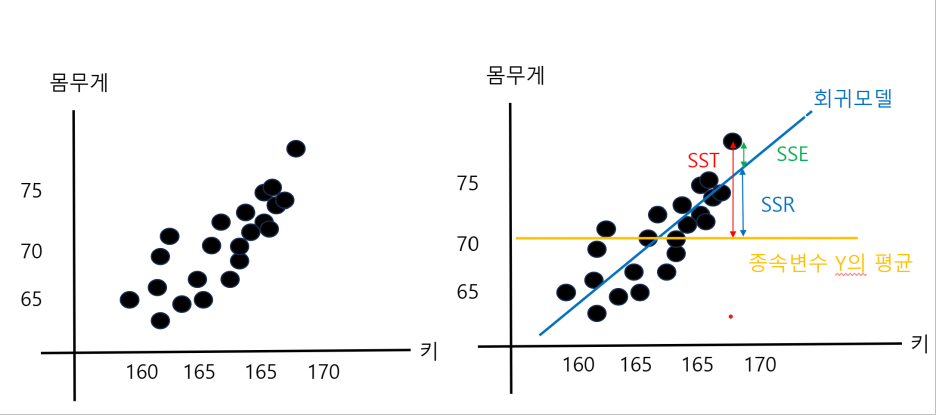
우리가 왼쪽과 같은 데이터를 가지고 오른쪽의 선형회귀모델선을 하나 만들었다고 가정 하였을때
R²는 실제 종속변수 Y값의 분산과 비하여 우리가 만든 회귀모델 값들의 분산이 얼마나 Y값의 분산과 유사한지를 판단한다고 볼 수 있다.
즉 분산을 통하여 Y값들과 모델이 얼마나 유사한가를 보는것이다.
각각의 용어들의 정의와 식은 아래와 같다.

위에서 이야기 하였듣이 Y값분산 대비 우리가 만든 모델의 분산이 얼마나 유사한지를 보기 때문에
R² = SSR/SST = 1 - SSE/SST와 같게 되는 것이다.
R²의 특징 및 유의점
- R²는 위에서 종속변수와 모델 분산값의 비율을 나타내기 때문에 0~1 사이의 값을 가지게 되고 1에 가까울수록 좋은 모델이라고 판단 할 수 있다.
2. 높은 R²가 무조건 좋은것은 아님!
- 독립변수의 개수가 추가 될수록 R²는 증가함
→ 의미없는 독립변수가 추가 되더라도 모델의 분산은 조금이라도 증가되기 때문에 R²값이 증가 하게된다.
→ 보완을 위해 독립변수의 수와 표본의 수를 활용한 Adjusted R² 가 있다.
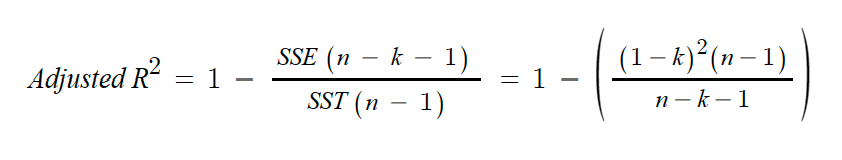
※ n = 표본의 수, k = 모델에서 사용된 독립 변수의 수이다.
우리가 사용한 키, 몸무게의 경우 각각의 점들이 표본이고 n 은 점들의 개수 이며 독립변수는 '키' 변수 1개 이기때문에 1이 될것다. 몸무게는 종속 변수!!
3. 여러 선형회귀모델을 만들었을때 R²의 값이 같다면 더 좋은 모델이란?
- 독립변수의 수가 적은 모델
4. 단순선형회귀(독립변수가 1개인 모델)의 경우 R²는 상관계수의 제곱과 같다.
5. R²값과 다른 평가 지표를 함께 사용하는것이 좋다.
- 회귀모델이 적절한데 R²가 낮을 수도 있고, R²가 높더라도 모델이 적절하지 않을수도 있기 때문
다른 평가 지표
MSE, RMSE, MAE, MAPE
Error = 오차 : 실제 y값과 모델의 예측값의 차이
MSE = Mean Squared Error
RMSE = Root Mean Squared Error
MAE = Mean Absolute Error
MAPE =Mean Absolute Percetage Error
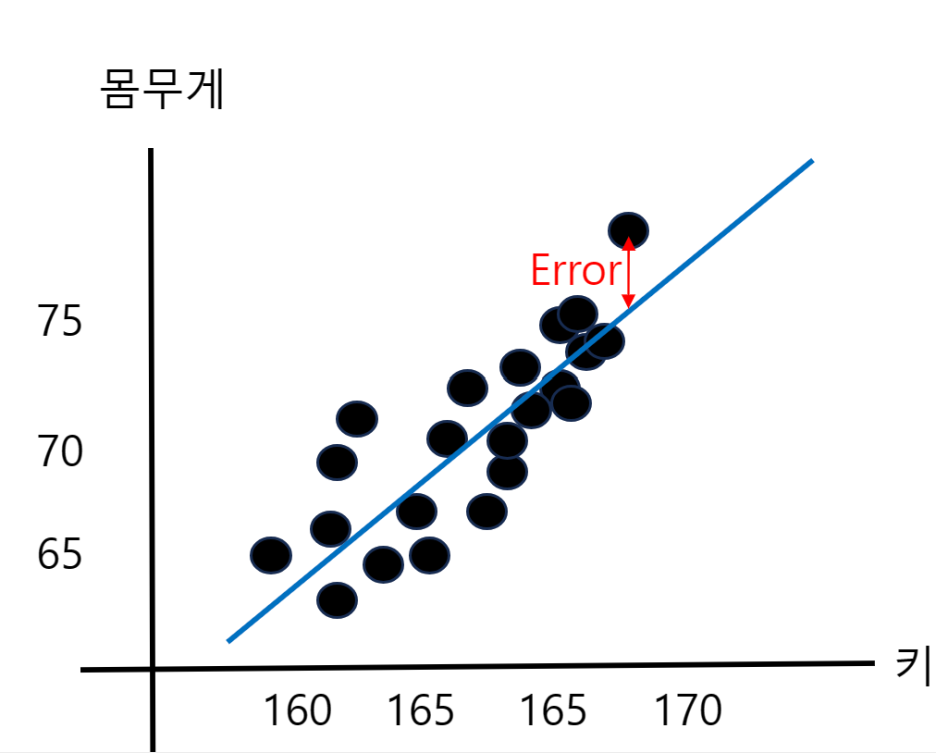
위의 실제 값들과 회귀 선의 차이를 이전에 Error 라고 하였는데 Error란 좀더 자세하게
표현 하자면 x가 동일 할때 우리가 만든 모델의 예측한 값과 실제 값의 차이를 얘기 한다.
