지수 분포란?
지수 분포란 특정 사건이 포아송 분포를 따르고 있을 때, 사건이 일어날때 까지의 대기시간을 나타낸다.
즉, 특정 단위시간에 평균 n회 일어나는 사건이 있을 때, 다음 사건이 일어날 때까지 대기 시간은 지수분포를 따른다.
이 분포를 활용하여 우리는 사건이 발생할때 까지의 걸리는 시간이 특정 시간 이하일 확률을 알 수 있다.
예를 들어 하루에 평균 n잔의 커피를 구매한다고 하였을때 사건이 발생하는 t 까지의 걸리는 시간이 T이하일 확률을 지수 분포를 통하여서 알 수 있다.
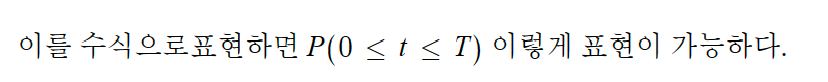
하루 평균 2잔의 커피를 마실때 커피를 마실때 까지의 걸리는 기간이 T 이하일 확률을 알고 싶다고 할 때
T를 3일 이라고 가정한다면,
하룻동안 커피를 마시지 않을 확률을 포아송 분포의 수식에 대입하여 13.5 %란 값을 얻을수 있다.
이를 3번 곱하면 0.24%를 얻을 수 있고 이를 통하여 3일 이하일 확률은 100 - 0.24를 대입하여 99.76%라고 할 수 있다. 즉 커피를 하루평균 2잔 마시는 사람이 3일 이내로 커피를 마실 확률은 99.76%라고 할 수 있다
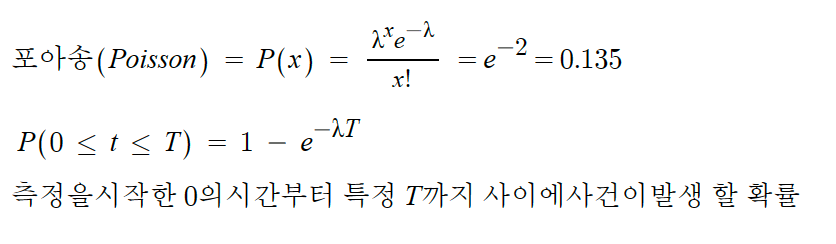
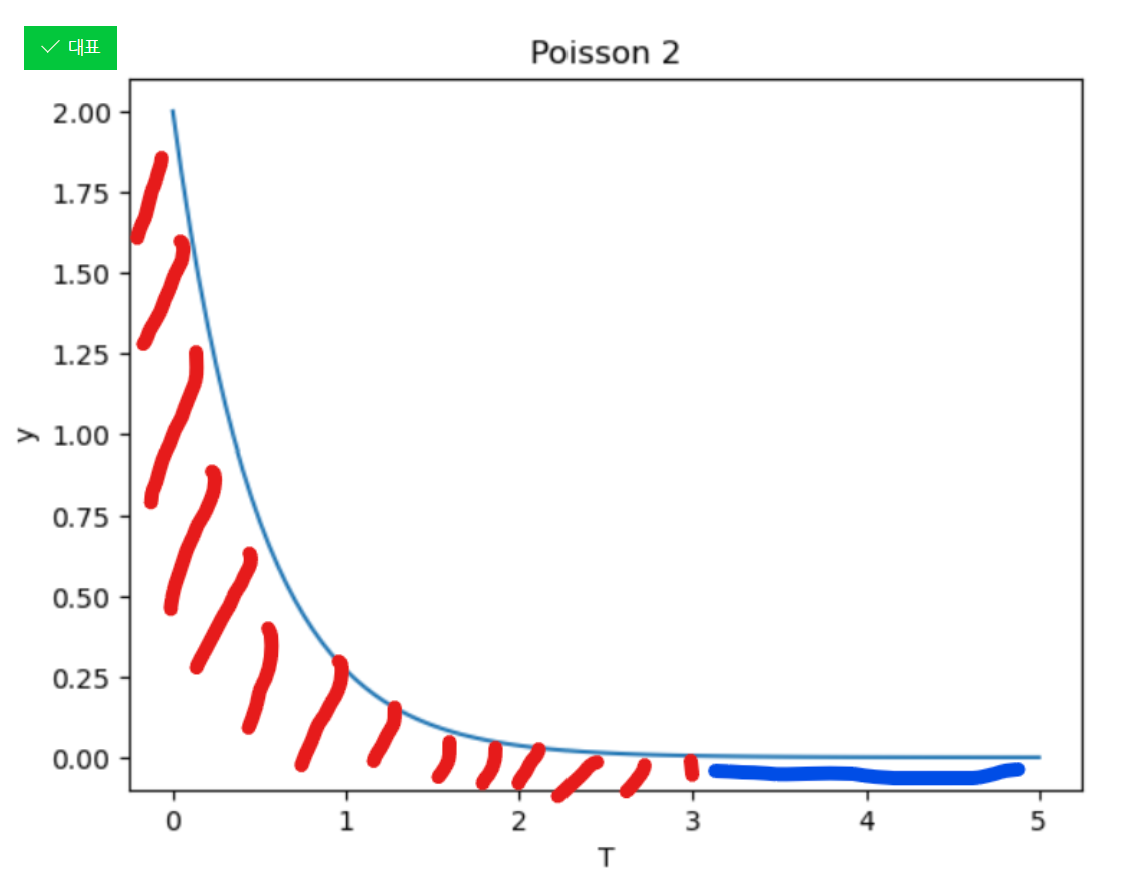
지수 분포를 그래프로 표현 하면 위와 같은 그래프가 나오는데, 우리가 궁금해하는 T가 x축이 되고
위의 예시에서 말했던 단위시간 3일 이내에 커피를 마실 확률의 그래프의 하방 면적이 된다.

지수 분포의 특징
지수 분포는 연속 확률 분포이고, 단위 시간에 따라 표현됩니다.
포아송 분포를 따르는 사건이 일어날 대기시간의 확률이기 때문에 항상 양의 값을 가지며
오른쪽 꼬리 긴 분포를 가지는게 특징입니다.

무기억성
지수분포에는 아직 발생하지 않은 상태에서 그 다음 사건이 발생할때 까지의 대기 시간의 확률은 항상 일정하다는 특징이 있습니다.
위에 커피를 마시는 것을 예로 들어보면
하루 평균 2잔의 커피를 마셨을때 3일 이후에 마실 확률은 99.76% 라고 하였다.
그런데, 측정을 커피를 마신 직후 부터 하던지, 1일차에 하던지 2일 차에 하던지 측정을 기준으로 3일 이후에 마실 확률은 동일하게 99.76%라는 얘기이다.
즉, 이전에 내가 얼마나 대기시간을 가졌는지 기억하지 못한다라는 성질!