로지스틱 회귀분석
이진 분류에 사용되는 로지스틱 회귀 분석의 설명 및 회귀 분석에 사용 되는 개념 설명입니다.
로지스틱 회귀 분석이란?
우리가 예측하려고 하는 종속변수가 연속 확률 변수가 아닌 이산 변수 혹은 명목형 변수라면 우리는 종속변수를 선택을 해야된다
즉, 독립 변수 x가 주어 졌을때 족립변수 y가 A, B중 무엇인가? 를 예측 하기 위한 회귀 분석 모델이다.
왜 로지스틱 회귀 분석을 사용해야 되는가??
우리가 이전에 배웠던 OLS 즉, 선형회귀 분석은 독립 변수 x가 주어 졌을때 종속변수를 연속형 변수로 예측 할수 있는 모델이기 때문에 A와 B중 하나를 선택 하기엔 적합하지 않다고 볼 수 있다.
혹은 종속 변수가 이산 변수 이고 두 변수가 1과 100 이라면 독립 변수 x가 주어 질때 x의 범위가 1~1000 이라면 OLS에서 사용하는 SSE를 적용하게 된다면 1보단 100으로 예측을 많이 하게 되기 때문에 로지스틱 회귀 분석을 사용 하여야 된다.
1) 종속 변수가 명목형 변수 혹은 이산변수 일때 사용
2) 선형 회귀 분석에서 SSE를 사용 하게 된다면 종속 변수가 이산 변수일때 판단이 어려워 질 수 있음
로지스틱 회귀 분석을 알기 위해선 우리는 승산비(오즈)와 로짓이 무엇인지 또 시그모이드 함수, 그리고 확률의 기초를 알아야 되는데 밑의 설명글을 통해 하나씩 알아 보자
승산 오즈(odds)란?
오즈란 영문 해석을 보면 승산 이라는 뜻으로 어느 한 사건이 일어날 승산 정도라고 생각하면 됩니다.
어떠한 사건이 일어날 확률은 0~1 까지 이다.
그때 사건이 일어날 확률은 p로 표기가 되고 일어나지 않을 확률은 1-p 로 얘기 할 수 있다.
이를 사건이 일어날 확률은 일어나지 않을 확률의 몇배인가를 우리는 승산이 얼마나 되는가로 표현한다.
ex) A팀이 이길 승산이 얼마야? → A팀의 이길 확률 / B팀이 이길 확률
사건 확률 P가 0~1까지 값을 가진다면 odds의 범위는 얼마일까? P에다가 0과 1을 대입한다면 odds의 범위는
0 ≤ odds ≤ ∞ 을 가지게 된다.
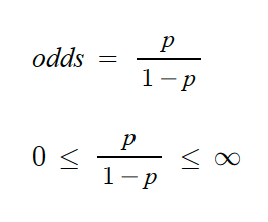
이게 승산(오즈)의 전부이다. 그럼 오즈가 0 부터 무한 까지 가진거랑 로지스틱 회귀 분석이랑 무슨 상관이야?
라고 할 수있는데 아래의 함수를 보면 필요한 이유를 알 수 있게 된다.
시그 모이드 함수
시그 모이드 함수 란?
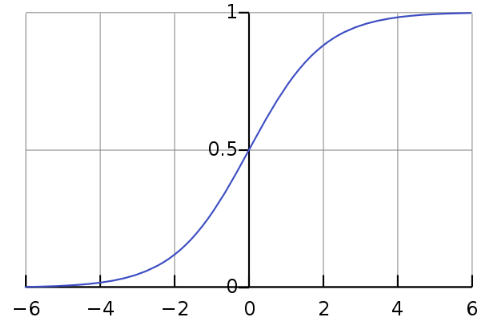
위의 그림을 보면 독립변수 x가 0일때 0.5의 값을 가지고 x의 범위가 - ∞ 에서 ∞ 일때
종속 변수 y가 0부터 1의 사이 값을 가지는 함수 인데 이 함수의 식은
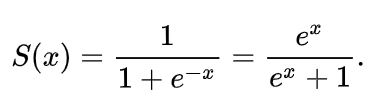
위의 식과 같은 계산식을 가지게 된다.
우리가 위에서 구한 승산은 독립 변수 x를 가졌을때 값을 0 부터 ∞ 을 가진다고 하였는데 독립 변수를 - ∞ 부터 ∞을 가지게 한다면 우리는 시그 모이드 함수를 활용하여 종속 변수를 0~1 사이의 값을 가지게 만들 수 있고 이 값을 활용하여 0.5 이상이다면 A 이하면 B 라고 예측 할 수있게 되고 이때 0.5는 기준선 threshold 라 불리며 이값은 사용자가 임의로 조정 하여 결과 값을 예측 할 수있다.
ex) y값이 0.6 이상이면 A 보다 작으면 B로 판단한다
그렇다면 이제 x의 범위를 0 ~ ∞ 을 - ∞ ~ ∞ 으로 가지게 해보자
logit 이란?
승산의 범위가 0 ~ ∞ 일 때 이 값들에게 log를 씌운다면 각각의 값은 어떻게 될 것인가?
0의 log는 - ∞ 이 되고 ∞ 로그는 ∞ 이다.
즉 승산에 log를 씌우게 된다면 우리는 종속변수의 범위를 - ∞ ~ ∞ 으로 가질 수 있게 할수 있다.
이를 함수로 표현하게 된다면
