t 분포표란 가설검정중 하나인 t-test, t검정이라고 불리는 검정에서 참고할 분포표로 아래그림과 같이 생겼습니다.
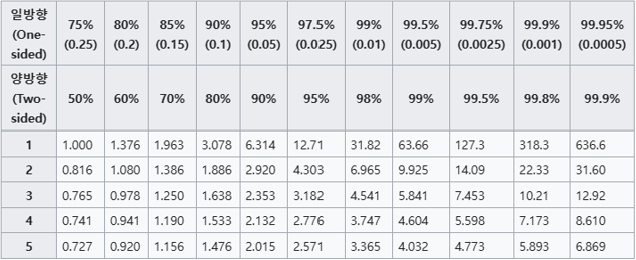
분포표에서 X축 방향으로 일방향(One-tail)과 양방향(Two-tail)이 보이고, Y축 방향으로 1,2,3,4 등이 보이네요.
그리고 X,Y 사이에 각각의 값들이 보입니다.
제 나름대로 하나의 예시를 통해서 X 축 방향의 일방향과 양방향의 차이를 알아 보겠습니다.
우선 이름에서 알 수 있듣이 일방향 테스트는 단측 검증에 사용되고, 양방향은 양측 검증에 사용됩니다.
우리가 통계학에서 t-test를 하는 이유는 대립가설과 귀무가설의 채택 여부를 확인 하기 위해서 이고 이는 두 집단의 평균의 차이가 우연히(?) 일어 날 만한지 아닌지를 검정한다고 할 수 있습니다.
단측검증.
약효를 예로 들 수 있겠네요.
가령 감기를 걸린뒤 자연 치료 되는데 보통의 사람들이 10일이 소요 된다고 하였을 때, A라는 약을 복용 하였을때 치료가 되는것을 가정해보겠습니다.
우리가 약을 먹음으로써 알려진 사실 10일 보다 빨리 나을 것이라는것을 모두 기대를 하고 있고 일반적인 상식선에서 10일 이상으로 오래 가면 안된다는것을 알고있습니다.
이럴 경우 A < 10 인 경우만 우리는 검증을 하면 됩니다 . 즉, A가 10일 이상인지 이하 인지가 아닌 A 가 10일 이하인 경우만 구해야 될 경우 우리는 단측 검증 즉 일방향을 기준으로 분포표를 보아야 됩니다.
양측검증.
A대학과 B대학의 키차이를 알 고 싶다고 가정해보겠습니다.
A의 평균은 180이 나왔고 B의 평균은 178이 나왔습니다. 발생한 평균의 차이는 2가 나왔을때 2가 우연히 나왔는지 아닌지를 가설검정을 통해 알아 볼것입니다. 이러할 때 A와 B대학의 평균의 차이는 2이다 아니다가 될 것인데
이를 다르게 설명하면 2보다 크거나 작거나 X < 2 < X 가 될 것 입니다.
이러 할때 양측 검증, 양방향을 기준으로 분포표를 보아야 됩니다.
자유도
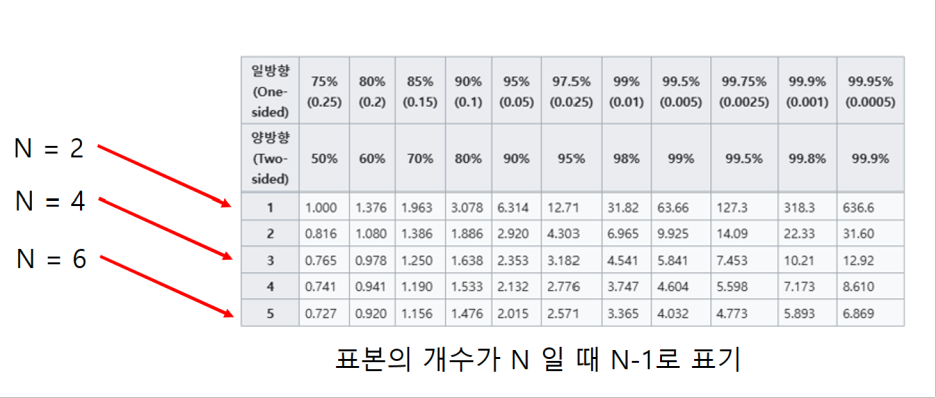
y축은 자유도라고 불리우는 축인데 쉽게 설명하면 표본의 갯수가 n이라고 할때 n-1을 자유도 df라고 합니다.
t 분포표
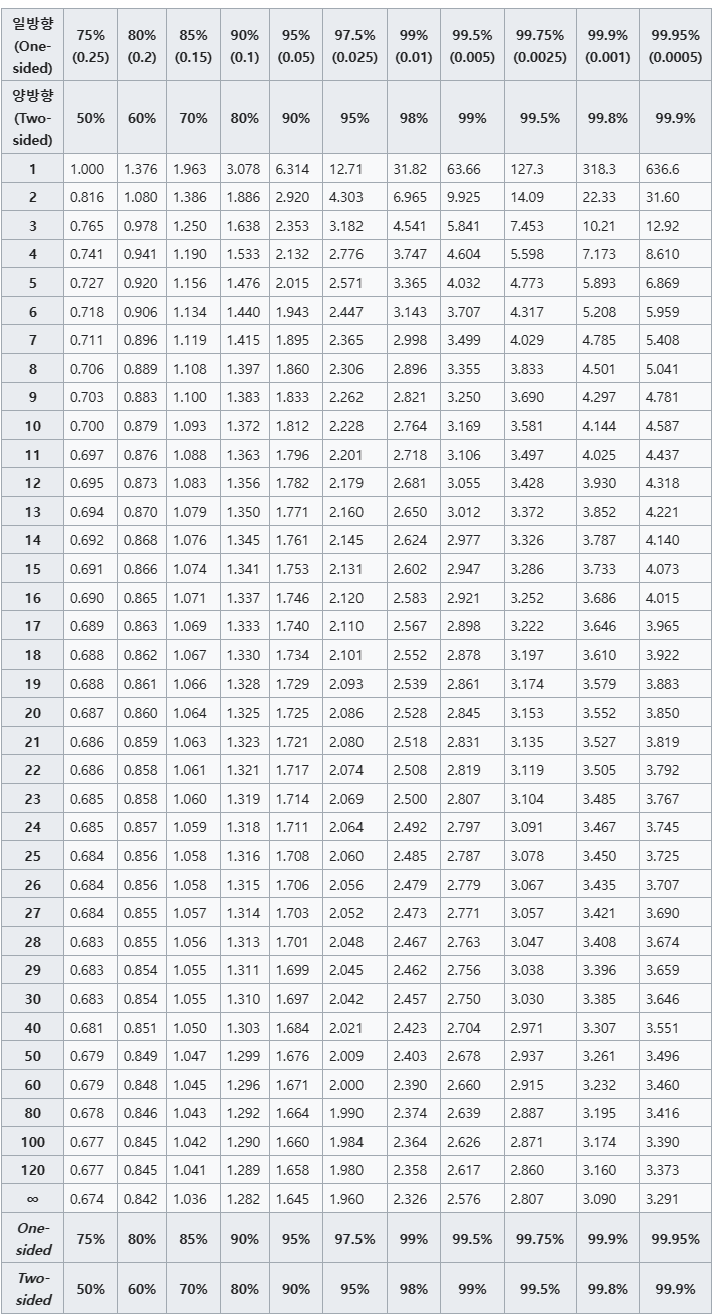
t 분포표 활용 하여 예제를 풀어 봅시다.
문제.
1. 방향 검증을 하고 표본의 개수가 20개였을때 t-test 값이 2.1이 였을때 귀무가설과 대립가설의 채택 여부의 유의수준을 0.05로 설정하고자 한다. 그럴 때 귀무가설이 채택이 될 것인가 대립가설이 채택 될것인가?
2. t-test의 결과가 10 이상인 경우에 대해 귀무가설이 채택 될지 대립가설이 채택 될지를 알 고자 한다.
유의수준은 0.1로 설정하고자 하고 표본의 개수는 30개 이고 t-test 값이 1.311 이라면 이 차이는 유의 한가 아닌가를 귀무 가설과 대립가설의 채택 여부로 대답 하시오.
해설.
1. 문제에서 주어진 값은 표본의 개수는 20 = 자유도는 19를 의미하고, 유의 수준 0.05는 분포표의 95% 안에
결과값이 들어오면 해당 결과는 귀무가설을 채택 하겠다는 내용입니다.
자유도가 19에 95%의 결과 값을 위 표에서 찾으면 2.093이 나옵니다. 2.1 보다 작네요.
즉 저희가 구한 t value 는 95% 범위를 벗어난 값이 된 겁니다. 그럼 유의수준 0.05를 기준으로 해당 결과는
귀무가설이 기각 되고 대립 가설이 채택 되게 됩니다.
2. 문제에서 주어진 값은 결과가 한쪽방향으로만 알아야되는 경우 즉 일방향 검증을 test 한다고 나와 있습니다.
또한 자유도는 n-1로 29라고 나옵니다. 유의 수준은 0.1로 90%에 대한 값을 찾으면 되네요!
그럼 자유도 29의 일방향 검증의 90%에 해당하는 값은 얼마인지 위 분포표를 보면 1.311이 나오네요
저희가 구한 값과 동일하네요 이러한 경우 90% 이내에 들어 왔기 때문에
결과는 귀무가설 채택 대립가설 기각입니다.